Sketching a language for Web Programming (Part II)

This is the second episode of my ramblings about web programming I started here.

Previously, I sketched a sort of graphical language to define user interfaces and their dynamics. The work is inspired by Milner’s bigraphs [1] and the final goal is to come up with an operational semantics in the style of signal flow graphs [2] or a new web framework or both.

Here, I want to jot down some notes about composition.

In this post I will introduce new concepts. I ask to forgive me in advance if my treatment is still quite vague and inaccurate. The aim of these notes is to refine my own intuition before working on a more formal approach.

Components

A component $F$ is a “data structure” with a type $A \to B$. The type $A \to B$ consists of two other types $A$ and $B$. Think about types as interfaces that help us to compose components together.

If you know a bit of Category Theory, you should see that a component is a morphism. What is a morphism? First, it is not a function. Not necessarily at least. A morphism is like a Lego brick. A Lego brick is a shape with two interfaces (bottom side and top side). Interfaces can have different types $2 \times 4$-bottom or $2 \times 4$-top (e.g. the brick sizes). We can put together Lego bricks if their interfaces match. That is all you need to know for now.

As I discussed in my previous post, we can see a web application in two independent ways: a spatial part (dom) and a dynamic part (communication or data dependencies). Hence, it can be represented by two data structures.

The spatial part is represented as a tree. Trees have interfaces we call roots and sites. Intuitively, we can compose two trees plugging roots into sites.

In React components have only one root (i.e. the output of the render function), but it is convenient to define components as a collection of trees, each with its own root. Sites are similar to the concept of slot in Vue or even children prop in React. So we are not inventing anything new.

The dynamic part connects dom elements to states and defines a sort of dependency graph. When a state changes, we expect some updates in UI elements. React and Vue implement inter-component communication using the Flux pattern or, in general, the programmer defines the mechanism behind state change. Here, we do not want to say how state changes, but what changes. It could be closer to MobX or transparent reactivity in Meteor.

So, more precisely, a component $F$ has type $(n, X) \to (m, Y)$ where $n, m \in \mathbb{N}$ and $X, Y$ are finite sets of names. Intuitively, $F$ is a piece of user interface with $n$ sites and $m$ roots. It has an outer interface $Y$ and an inner interface $X$. Definitions and terminology are from bigraphs, as usual.

Internally, $F$ is represented with two data structures: a tree-like structure for the dom hierarchy and some linking between node ports for communication. The picture below shows a generic component with type $(2, { x }) \to (1, { y })$.

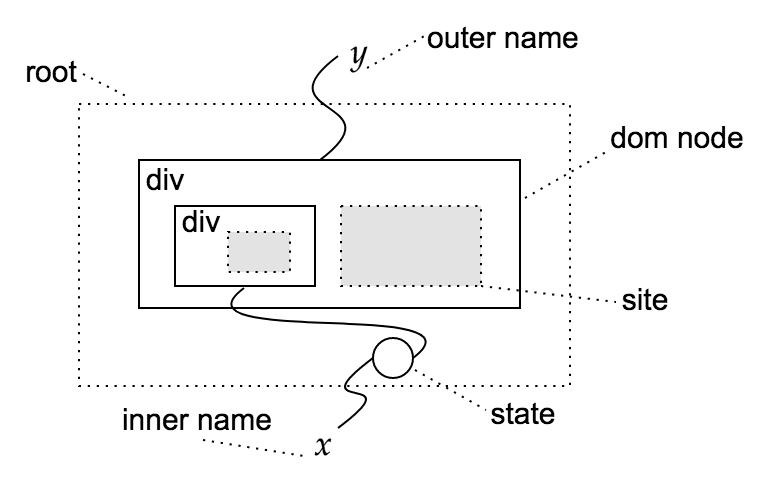
A simple stateless button

Let’s consider a button $B_0: (0, \emptyset) \to (1, { \mathit{event}, \mathit{handle} })$.

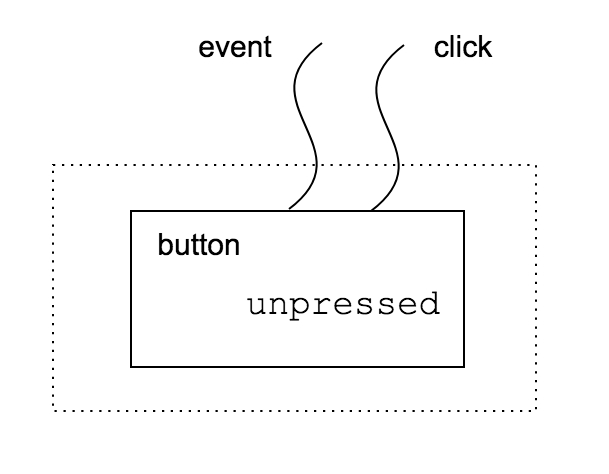
A button is a single dom element and can be plugged into an available slot in a larger context. So it has one root and no holes. For example, we can put a button inside a div element. A button has an outer interface with two elements to communicate with the world: $\mathit{event}$ and $\mathit{handle}$.

Intuitively, $\mathit{event}$ listens to dom events whereas $\mathit{handle}$ triggers a response to a dom event. However, a button is not a function, but a relation between events and handlers. We will see it when we discuss operational rules.

Components are views plus states

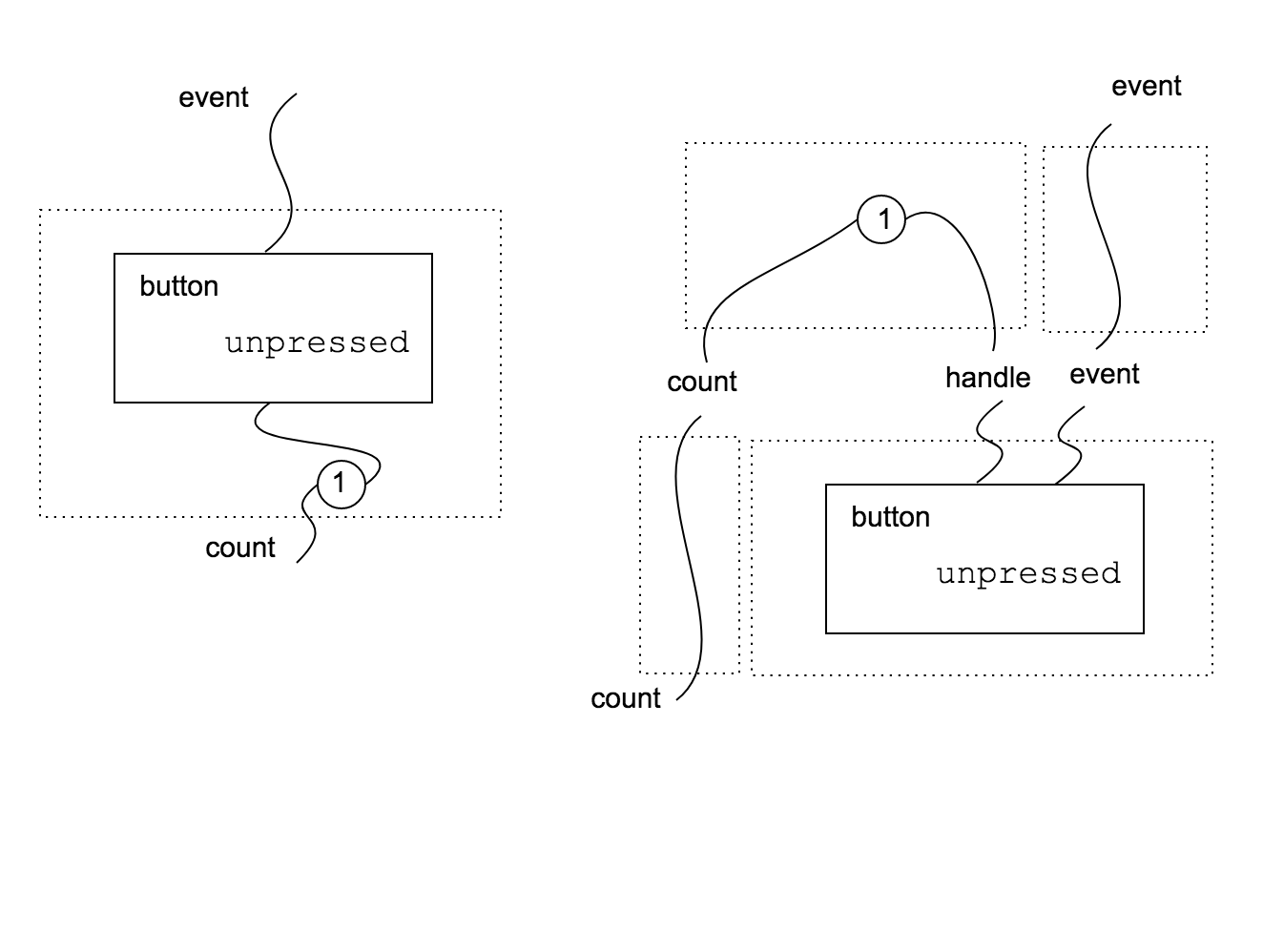
A component is not only a view like in the case of $B_0$. For example, we can define a counter button $B_1: (0, { \mathit{count} }) \to (1, { \mathit{event} })$ that emits an increasing sequence of numbers at each click. We need an internal state to store the number of clicks. We use the inc state we introduced here.

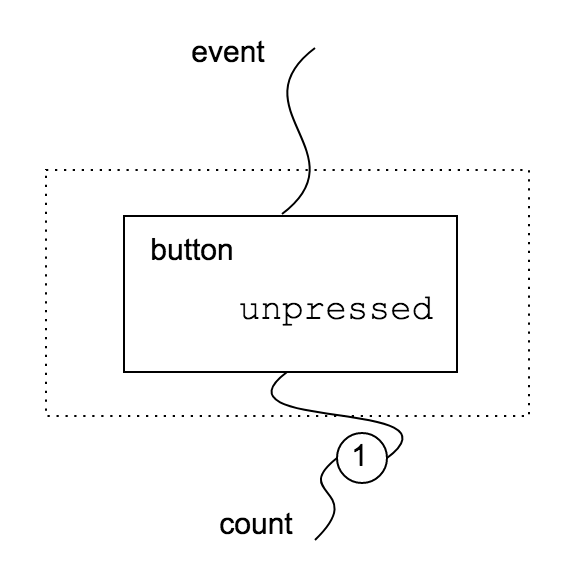
In this case, the main difference is that $B_1$ has a non empty inner interface ${ \mathit{count} }$. This means that $\mathit{count}$ depends on a state defined in component $B_1$ or in its context. On the contrary $\mathit{event}$ depends on the outer context (for example, the actual dom).

Components are cross-functional features

Microfrontends is an emerging trend in web development [3]. In this paradigm, a component, i.e. the unit of composition, is a cross functional feature. This is different from React and other frameworks where components are smart chunks of HTML; they implements a functionality (e.g. the navbar basket), not a use case (e.g. I want to purchase a fuzzy cat).

For example, in a web shop, Team F can implement use case “add to basket” as a component $F: (0, \emptyset) \to (2, { \mathit{product} })$ while Team G works on $G: (2, { \mathit{product} }) \to (1, \emptyset })$ component for use case “show product”.

Team F and Team G work independently. In particular, Team F provides all the logic needed to implement the use case “add to basket”. The same component $F$ with its views and states can be reused in a context different from $G$, for example, if we want to add an additional purchasing option in the checkout page.

We do not give a full description of the two states and their rules here, because we want to focus only on composition now. We leave to the reader the not so hard task.

Components are black boxes

In the above picture the product component does not show all the details of its implementation. Components are black boxes and they interact only through thier interfaces. For this reason, even if it might look complicated to draw lines from states to views and back, we do not have to see all the wiring in practice.

In other words, we can zoom in and out depending on the level of abstraction we are interested in. The min zoom level is the whole application. An application is just another component. Instead the max zoom level is a button or a more complex component. We can work on sub-components without worrying about the context.

In my opinion, React does not reach this level of compositionality. Quite the contrary. Sometimes state information leaks from components and it is hard to move components around without changing their implementation, in particular their states.

Zooming concept is similar to CycleJS “fractal” property. Actually, I rather have in mind [4] (spotted many years ago on some CT blog (Baez?)). I will write about CycleJS sooner or later.

Composition

In React types are used to specify the shape of props. In other words, types tell us if we invoke render functions with the proper values as arguments. Moreover, we can verify (only at run time) if a component has just one child.

In general, however, types can be more powerful. They can help us to compose components in such a way that we are a bit more certain that the whole web application behaves as expected.

For example, we want to be sure that a parent component takes the correct number of children or that a component’s dependencies are provided by the context where it is plugged in. These checks should be at compile time. In other words, we use types to guide the composition of components in a web application.

Let’s see how composition is defined for dom elements and dependencies. This is more or less the basic idea of Milner’s bigraphs. As for bigraphs, the two faces of web applications share the similar algebraic/compositional properties (i.e. they are related to symmetric monoidal categories).

Dom composition

Dom is a hierarchy of nested elements. It defines “within”-relations between HTML tags and custom elements. We have two ways to compose dom elements: inserting one element into another (e.g. parent/child) or juxtaposing them (e.g. siblings).

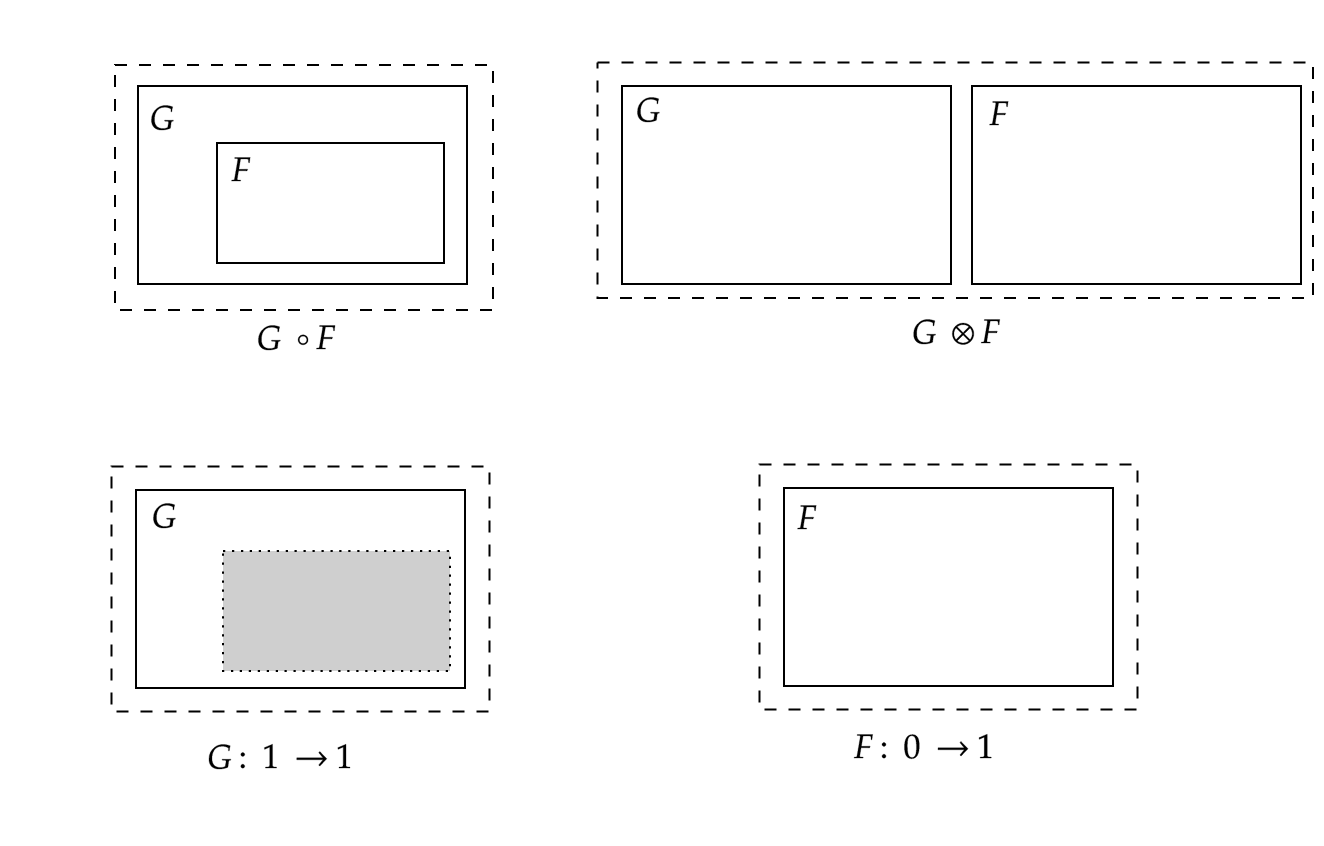
The picture above explains this concept. Dashed lines and gray boxes represent roots and sites, respectively. Composition $G \circ F$ is defined if $G$ and $F$ interfaces match.

Milner defines a data structure, i.e. place graphs, to describe this scenario and proves that place graphs are morphims in a sort of symmetric monoidal category (it is a bit more complex than this!). In this category nesting is morphism composition $\circ$ while juxtaposition is tensor product $\otimes$.

Dependency composition

In the previous section, we saw two ways to dispose components. There are other two ways: left/right and top/bottom.

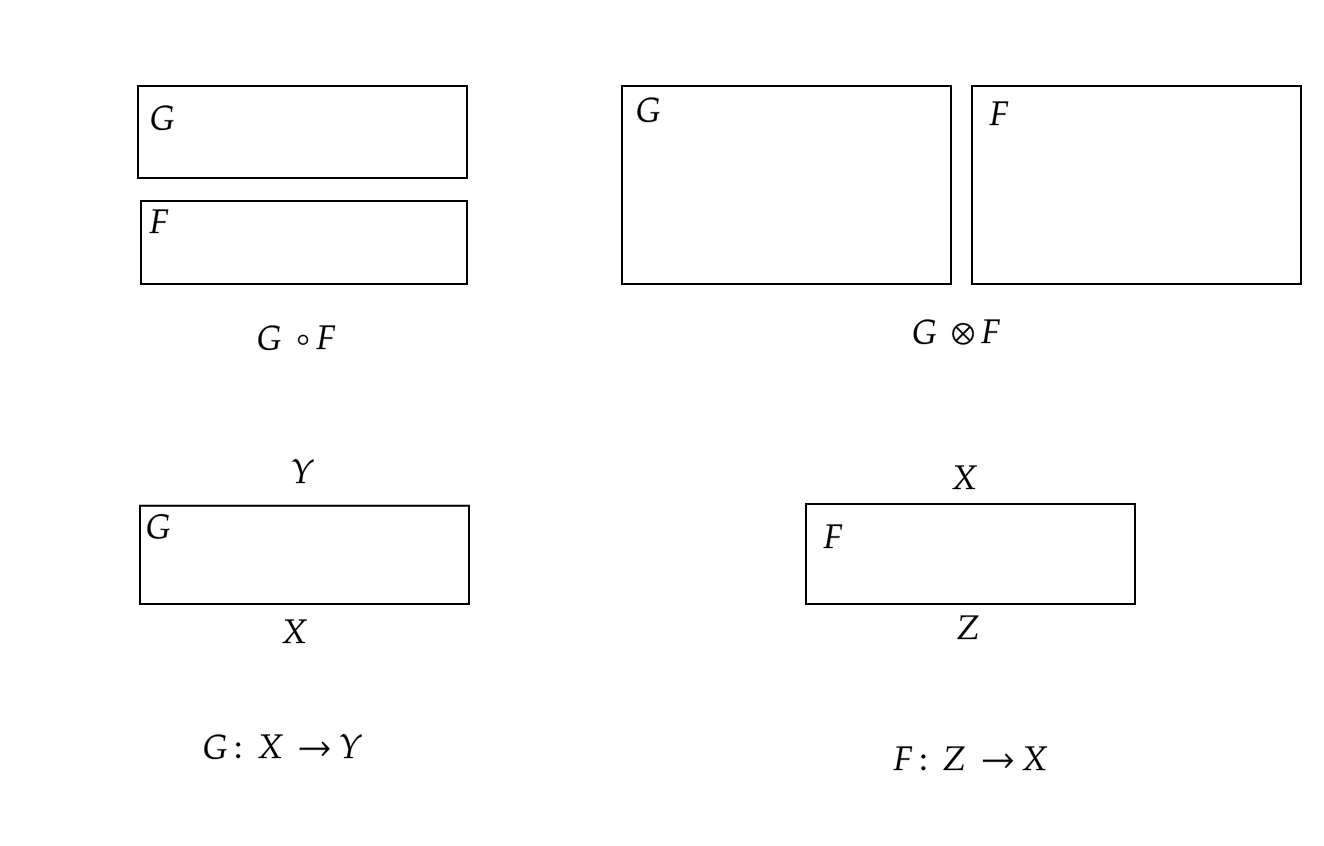
Above, we show the two ways to compose two components. Top and bottom sides are labeled with finite set of names for interfaces. Composition $G \circ F$ is defined only if interfaces match.

In bigraph, link graphs are the data structures that represent dependencies. Again link graphs are mortphims in a sort of symmetric monoidal category (and again, it is a bit more complex than this!). In this category top/bottom composition is morphism composition $\circ$ while right/left composition is tensor product $\otimes$.

Let’s go back to our example. Button $B_1$ can be obtained by composition of button $B_0$ with a state-only component. This is common in web programming. $B_0$ does not define what happens on click event, we need to bind the event with a function handler. Since we want to have generic reusable buttons, the handler logic is not part of the button definition. In the picture below we show how to build $B_1$ from simpler components. Note that composition is possible if inner and outer interfaces “match”. In this case we need to use two identity components.

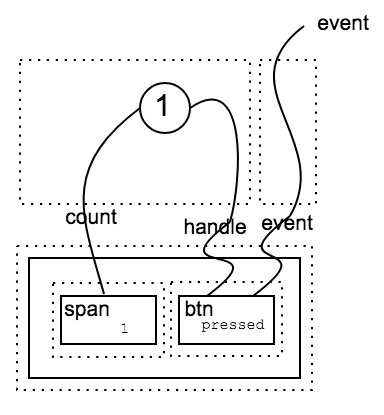
Building a counter

Finally, let’s try to put everything together and build a simplified version of the counter introduced here. Dotted boxes highlight basic blocks and we label links with outer/inner names. It should be clear how the full counter can be built from basic blocks using composition and tensor product for the two dimensions, namely, dependency and dom graphs.

Now, we can give a sample of operational derivation following the structure of the component. We follow [2]. Please, note that this is still tentative and many details must be clarified. What I want to sketch here is how we can describe the behavior of a simple web application from simple rules.

The derivation below is read top-down. Horizonal lines mean “deduction”. From transitions for basic blocks we derive a transition for the whole application following the application’s structure. For this reason, we talk about structural operational semantics. Two transitions for two sub components can be composed if their interfaces match. In this simple example, this happens when the same labels (in red) are assigned to the two components.

Coming soon

We have seen that bigraphs are three dimentional data structures, since we can define in/out, left/right, top/bottom spatial relations. I am going to introduce a forth dimension: a component can be in front of or behind another component. This dimension is independent from the other three (left/right, top/bottom, in/out).

I feel that this is needed to define the behavior of IF blocks. In other words, if a component $A$ is on another component $B$, $B$ transitions are hidden or disabled. In bigraphs morphisms can be active or passive. This is a similar idea. However, I would like to experiment what happens if activity does not depend on nesting (as in bigraphs), but it is an independent dimention.

Hence, if I am able to define this new concept, we need to think in four dimensions in order to build a web application. It is not surprising that front end programming is complex. ;)

Other episodes

• Sketching a language for Web Programming (Part I).

Credits

Diagrams in this post are created using Mathcha.

Cat clipart from here.

Lego brick from Wikimedia.

References

[1] Robin Milner. The space and motion of communicating agents. Cambridge University Press, 2009.

[2] F. Bonchi, P. Sobocinski, and F. Zanasi. Full abstraction for signal flow graphs. ACM SIGPLAN Notices. Vol. 50. No. 1. ACM, 2015.

[3] M. Geers, Microfrontends, 2016(?)-2018

[4] J.C. Willems. The behavioral approach to open and interconnected systems. IEEE Control Systems 27.6 (2007): 46-99.